Basics
Tutorials
Models
Inference
Verification
Theory
This notebook demonstrates the CUDA-accelerated likelihood function from the heron package. This likelihood function incorporates the variance from the waveform models in heron as well as the variance from the data.
[1]:
import math
import torch
from heron.models.torchbased import HeronCUDA
from heron.matched import CudaLikelihood
from matplotlib import pyplot as plt
import numpy as np
%matplotlib inline
Set up the model.
[2]:
generator = HeronCUDA()
For a smple demonstration, inject a signal into Gaussian noise.
[14]:
noise = 5e-19*torch.randn(1000)
signal = generator.time_domain_waveform({'mass ratio': 0.7}, times=np.linspace(-0.02, 0.02, 1000))
[15]:
from elk.waveform import Timeseries
[16]:
detection = Timeseries(data=(torch.tensor(signal[0].data) + noise), times=signal[0].times)
[17]:
plt.plot(detection.times, detection.data)
plt.plot(signal[0].times, signal[0].data)
[17]:
[<matplotlib.lines.Line2D at 0x7fbfd62a7630>]

Set up the likelihood object.
[18]:
l = CudaLikelihood(generator,
data = detection,
psd=noise.cuda().rfft(1),
)
[19]:
#%%timeit
masses = np.linspace(0.5,1.0,200)
likes = [l({'mass ratio': m}) for m in masses]
[20]:
masses[np.argmax(likes)]
[20]:
0.7738693467336684
[21]:
#plt.axvline([0.7], color='k')
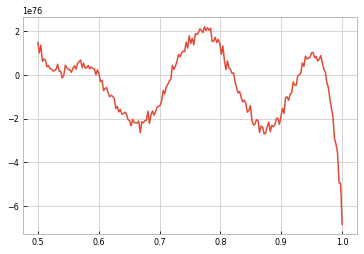
plt.plot(masses, likes)
[21]:
[<matplotlib.lines.Line2D at 0x7fbfd65c8b38>]
[43]:
l({'mass ratio': 0.2101})
[43]:
tensor(-2.0416e+36, device='cuda:0', dtype=torch.float64)
[44]:
l({'mass ratio': 0.92})
[44]:
tensor(1.7698e+35, device='cuda:0', dtype=torch.float64)
[45]:
l({'mass ratio': 1.0})
[45]:
tensor(1.0497e+35, device='cuda:0', dtype=torch.float64)
[44]:
size = 1000
times = np.linspace(-2, 2, 1000)
q = 0.9#masses[np.argmax(likes)]
points = np.ones((1000,2))
points[:,0] = times
points[:,1] = points[:,1] * np.log(q) * 100
test_x = torch.tensor(points).float()
test_x = test_x.cuda()
[45]:
#%%timeit
with torch.no_grad(), gpytorch.settings.fast_pred_var():
f_preds = model(test_x)
y_preds = likelihood(f_preds)
---------------------------------------------------------------------------
RuntimeError Traceback (most recent call last)
<ipython-input-45-b245066f9339> in <module>
1 #%%timeit
2 with torch.no_grad(), gpytorch.settings.fast_pred_var():
----> 3 f_preds = model(test_x)
4 y_preds = likelihood(f_preds)
~/.virtualenvs/gaston/sandbox/local/lib/python3.7/site-packages/gpytorch/models/exact_gp.py in __call__(self, *args, **kwargs)
307 train_input = train_input.expand(*batch_shape, *train_input.shape[-2:])
308 input = input.expand(*batch_shape, *input.shape[-2:])
--> 309 full_inputs.append(torch.cat([train_input, input], dim=-2))
310
311 # Get the joint distribution for training/test data
RuntimeError: invalid argument 0: Sizes of tensors must match except in dimension 0. Got 2 and 8 in dimension 1 at /pytorch/aten/src/THC/generic/THCTensorMath.cu:71
[ ]:
[ ]:
with torch.no_grad():
lower, upper = y_preds.confidence_region()
f, ax = plt.subplots(1,1, dpi=300)
ax.plot(test_x[:,0].cpu().numpy(), f_preds.mean.cpu().numpy()/1e21)
#samples = y_preds.sample_n(100)
#for sample in samples:
# ax.plot(test_x[:,0].numpy(), sample.numpy()[:,0], alpha=0.01, color='r')
# ax.plot(test_x[:,0].numpy(), sample.numpy()[:,1], alpha=0.01, color='b')
#ax.plot(training_x[:,0].cpu(), training_y.cpu()/1e21, '+')
ax.fill_between(test_x[:,0].cpu().numpy(), lower.cpu().numpy()/1e21, upper.cpu().numpy()/1e21, alpha=0.5)
[ ]:
generator.parameters
[ ]:
# We use SGD here, rather than Adam. Emperically, we find that SGD is better for variational regression
optimizer = torch.optim.Adam([
{'params': model.parameters()},
], lr=0.1)
# Our loss object. We're using the VariationalELBO
mll = gpytorch.mlls.ExactMarginalLogLikelihood(likelihood, model)
epochs_iter = tqdm.tqdm_notebook(range(training_iterations), desc="Epoch")
for i in epochs_iter:
optimizer.zero_grad()
# Output from model
output = model(training_x)
# Calc loss and backprop gradients
loss = -mll(output, training_y).cuda()
loss.backward()
optimizer.step()